Regression model
2021-03-30
Regression model for prediction
In this part, the data set Orange is used to show how regression could be used for prediction in food science.
Load data
Have a look at dataset Orange:
library(datasets)
orange <- Orange
head(orange)## Tree age circumference
## 1 1 118 30
## 2 1 484 58
## 3 1 664 87
## 4 1 1004 115
## 5 1 1231 120
## 6 1 1372 142Linear regression model
To establish the relationship Linear regression model between the circumference and age.
lm_model <- lm(circumference ~ age, data = orange)
summary(lm_model)##
## Call:
## lm(formula = circumference ~ age, data = orange)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46.310 -14.946 -0.076 19.697 45.111
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.399650 8.622660 2.018 0.0518 .
## age 0.106770 0.008277 12.900 1.93e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.74 on 33 degrees of freedom
## Multiple R-squared: 0.8345, Adjusted R-squared: 0.8295
## F-statistic: 166.4 on 1 and 33 DF, p-value: 1.931e-14To plot the Linear regression model:
coeff=coefficients(lm_model)
coeff## (Intercept) age
## 17.3996502 0.1067703# Equation of the line :
eq = paste0("y = ", round(coeff[2],1), "*x + ", round(coeff[1],1))
eq## [1] "y = 0.1*x + 17.4"Linear regression model plot
library(ggplot2)
# Plot
ggplot(data=orange, aes(x=age, y=circumference)) + geom_point() + geom_abline(intercept = 17.39, slope = 0.11, color="red",
linetype="dashed", size=1.5)+
labs(title= eq,x = "Age", y = "circumference") +
theme_bw()+
theme(
plot.title = element_text(color="black", size=16, face="bold.italic"),
axis.title.x = element_text(color="black", size=14, face="bold"),
axis.title.y = element_text(color="black", size=14, face="bold"))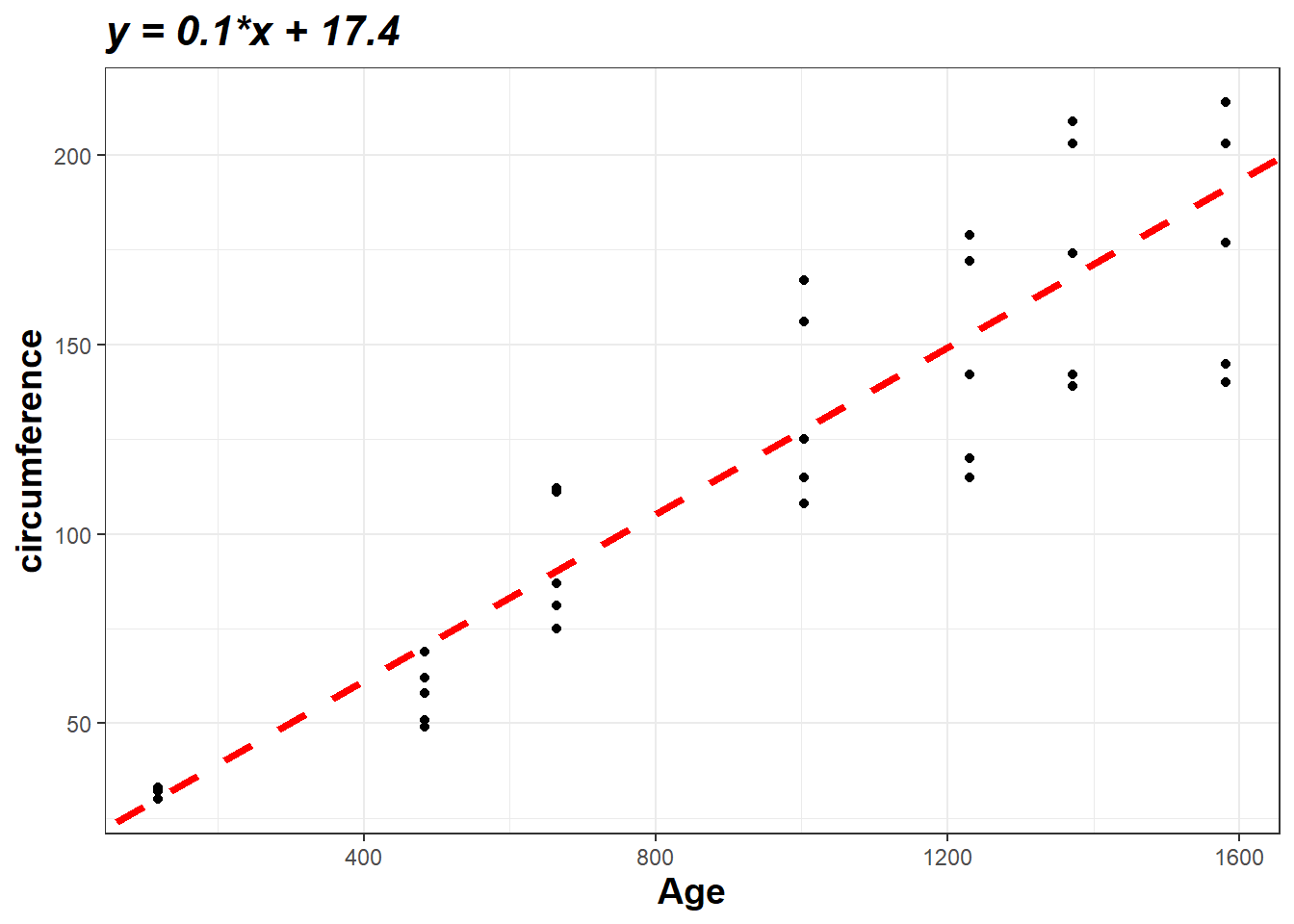
Then, you can use formulas to do some simple forecasting work, of course, you can also directly call the model for calculations. Here is an example:
the simple prediction example
To predict the weight based on time and diet types using dataset Chick weight
library(performance)
Chick_data <- ChickWeight
str(Chick_data)## Classes 'nfnGroupedData', 'nfGroupedData', 'groupedData' and 'data.frame': 578 obs. of 4 variables:
## $ weight: num 42 51 59 64 76 93 106 125 149 171 ...
## $ Time : num 0 2 4 6 8 10 12 14 16 18 ...
## $ Chick : Ord.factor w/ 50 levels "18"<"16"<"15"<..: 15 15 15 15 15 15 15 15 15 15 ...
## $ Diet : Factor w/ 4 levels "1","2","3","4": 1 1 1 1 1 1 1 1 1 1 ...
## - attr(*, "formula")=Class 'formula' language weight ~ Time | Chick
## .. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
## - attr(*, "outer")=Class 'formula' language ~Diet
## .. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
## - attr(*, "labels")=List of 2
## ..$ x: chr "Time"
## ..$ y: chr "Body weight"
## - attr(*, "units")=List of 2
## ..$ x: chr "(days)"
## ..$ y: chr "(gm)"chick_model <- glm(weight ~ Diet + Chick + Time, family = poisson, data = Chick_data)
summary(chick_model)##
## Call:
## glm(formula = weight ~ Diet + Chick + Time, family = poisson,
## data = Chick_data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.9303 -0.9988 0.1032 1.0588 4.7417
##
## Coefficients: (3 not defined because of singularities)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 5.2142670 0.1936690 26.924 < 2e-16 ***
## Diet2 -0.9717217 0.1144993 -8.487 < 2e-16 ***
## Diet3 1.3961015 0.5147568 2.712 0.006685 **
## Diet4 -7.3644551 1.2491116 -5.896 3.73e-09 ***
## Chick.L 14.3300412 2.1141495 6.778 1.22e-11 ***
## Chick.Q 10.3660415 2.1707311 4.775 1.79e-06 ***
## Chick.C 6.5867037 1.4139851 4.658 3.19e-06 ***
## Chick^4 0.1957681 0.2660284 0.736 0.461797
## Chick^5 -5.9204259 1.1777063 -5.027 4.98e-07 ***
## Chick^6 -5.6813376 1.0949784 -5.189 2.12e-07 ***
## Chick^7 -0.4267480 0.0785856 -5.430 5.62e-08 ***
## Chick^8 4.2201395 0.7623384 5.536 3.10e-08 ***
## Chick^9 3.5606073 0.6925422 5.141 2.73e-07 ***
## Chick^10 0.2514637 0.1742330 1.443 0.148947
## Chick^11 -1.6488925 0.3198935 -5.155 2.54e-07 ***
## Chick^12 -1.7609231 0.3884237 -4.534 5.80e-06 ***
## Chick^13 -1.1886304 0.2576511 -4.613 3.96e-06 ***
## Chick^14 -0.2707554 0.0580297 -4.666 3.07e-06 ***
## Chick^15 0.9199575 0.1983839 4.637 3.53e-06 ***
## Chick^16 1.6925734 0.3454127 4.900 9.58e-07 ***
## Chick^17 1.3691964 0.2817563 4.860 1.18e-06 ***
## Chick^18 -0.0060412 0.0739866 -0.082 0.934923
## Chick^19 -1.9397543 0.3642756 -5.325 1.01e-07 ***
## Chick^20 -1.8873827 0.3709271 -5.088 3.61e-07 ***
## Chick^21 -0.2451929 0.0595112 -4.120 3.79e-05 ***
## Chick^22 1.3693293 0.2653593 5.160 2.47e-07 ***
## Chick^23 1.5186612 0.2958940 5.132 2.86e-07 ***
## Chick^24 0.6616671 0.1495740 4.424 9.70e-06 ***
## Chick^25 -0.3459052 0.0479419 -7.215 5.39e-13 ***
## Chick^26 -0.3651166 0.1319512 -2.767 0.005656 **
## Chick^27 -0.8880659 0.2000315 -4.440 9.01e-06 ***
## Chick^28 -0.9955606 0.1971092 -5.051 4.40e-07 ***
## Chick^29 -0.2213652 0.0624320 -3.546 0.000392 ***
## Chick^30 0.8015526 0.1662002 4.823 1.42e-06 ***
## Chick^31 1.5380575 0.3060660 5.025 5.03e-07 ***
## Chick^32 0.0653622 0.0311500 2.098 0.035878 *
## Chick^33 0.5237846 0.1018214 5.144 2.69e-07 ***
## Chick^34 0.8104925 0.1540562 5.261 1.43e-07 ***
## Chick^35 0.1908673 0.0384804 4.960 7.05e-07 ***
## Chick^36 0.3950183 0.0984192 4.014 5.98e-05 ***
## Chick^37 -0.2858399 0.0662086 -4.317 1.58e-05 ***
## Chick^38 0.9347898 0.1983377 4.713 2.44e-06 ***
## Chick^39 -1.8940642 0.3628030 -5.221 1.78e-07 ***
## Chick^40 -1.0019379 0.2318050 -4.322 1.54e-05 ***
## Chick^41 0.9302278 0.1930879 4.818 1.45e-06 ***
## Chick^42 -0.4850002 0.0751800 -6.451 1.11e-10 ***
## Chick^43 -0.8213460 0.1283893 -6.397 1.58e-10 ***
## Chick^44 0.4736133 0.0963959 4.913 8.96e-07 ***
## Chick^45 -0.9185178 0.1766278 -5.200 1.99e-07 ***
## Chick^46 -0.0974344 0.0535733 -1.819 0.068955 .
## Chick^47 NA NA NA NA
## Chick^48 NA NA NA NA
## Chick^49 NA NA NA NA
## Time 0.0753395 0.0006131 122.880 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 22444 on 577 degrees of freedom
## Residual deviance: 1438 on 527 degrees of freedom
## AIC: 5282.7
##
## Number of Fisher Scoring iterations: 4model_performance(chick_model)## # Indices of model performance
##
## AIC | BIC | Nagelkerke's R2 | RMSE | Sigma | Score_log | Score_spherical
## ------------------------------------------------------------------------------------
## 5282.750 | 5505.088 | 1.000 | 17.106 | 1.652 | -4.482 | 0.034The RMSE value of generalized linear model (GLM) model is quite high, which indicated the model should be improved using more data. We will use more suitable dataset for following examples.