The date from Vc contents of different fruits were used to perform ANOVA.

import seaborn as sns
import matplotlib.pyplot as plt
df.head(n=20)

##     Number       Fruit Repeat  Vitamin
## 0        1       Apple     A1      4.6
## 1        2       Apple     A2      3.9
## 2        3       Apple     A3      5.2
## 3        4       Apple     A4      6.9
## 4        5       Apple     A5      4.8
## 5        6       Apple     A6      3.3
## 6        7      Banana     A1      8.7
## 7        8      Banana     A2      8.8
## 8        9      Banana     A3     10.3
## 9       10      Banana     A4     11.5
## 10      11      Banana     A5     12.7
## 11      12      Banana     A6      9.6
## 12      13  Watermelon     A1      8.1
## 13      14  Watermelon     A2      8.5
## 14      15  Watermelon     A3      7.5
## 15      16  Watermelon     A4      8.4
## 16      17  Watermelon     A5     10.3
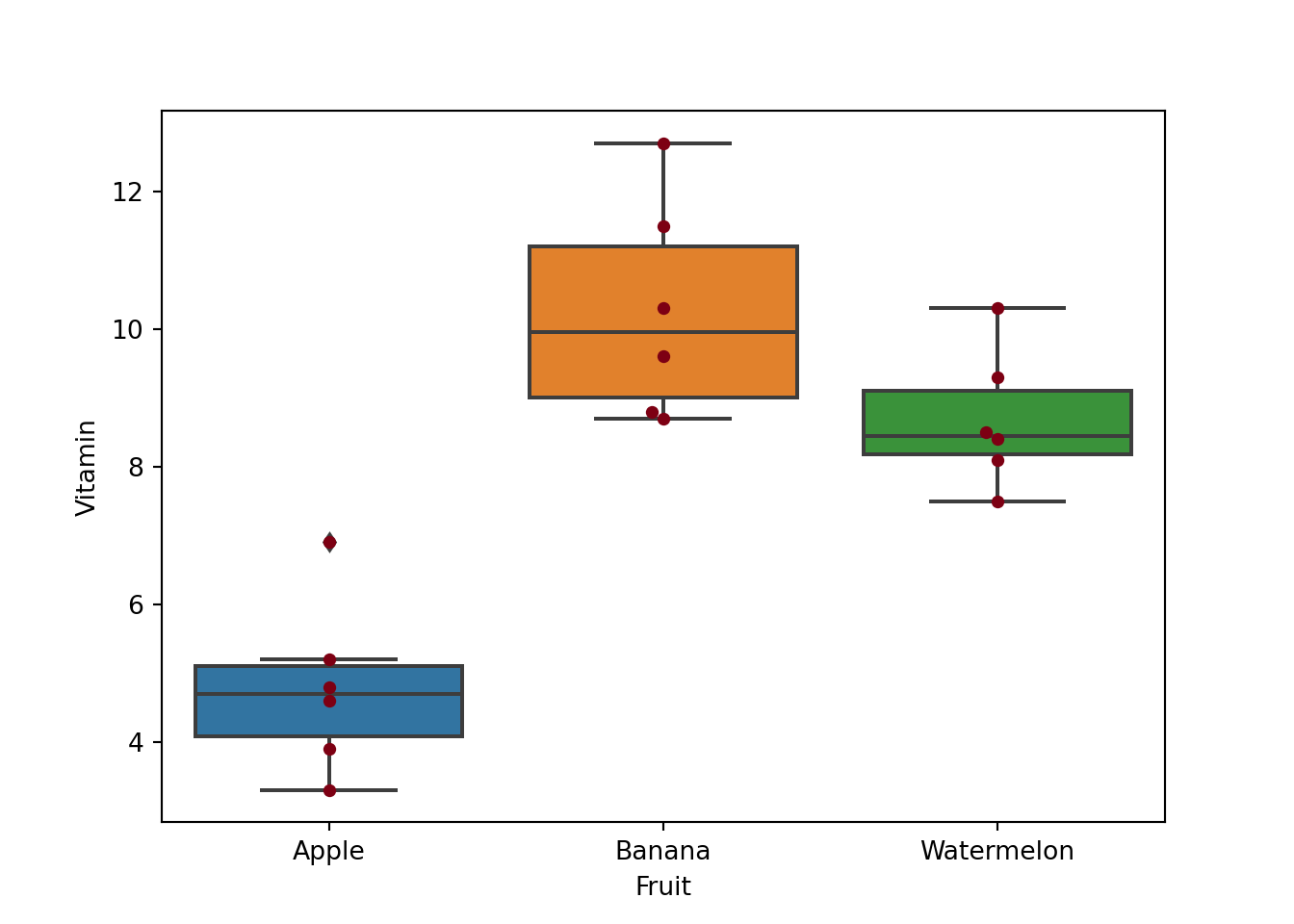
## 17      18  Watermelon     A6      9.3

To generate a box plot to see the data distribution by treatments.

plt_2 = sns.boxplot(x="Fruit", y="Vitamin",data = df)
plt_3 = sns.swarmplot(x="Fruit", y="Vitamin",data = df, color='#7d0013')
plt.show()

To show the results of mean SD values:

import scipy.stats as stats
# reshape the d dataframe suitable for statsmodels package 
df_wide=pd.pivot(data = df, index='Repeat', columns = 'Fruit', values = 'Vitamin') #Reshape from long to wide

# stats f_oneway functions takes the groups as input and returns ANOVA F and p value
df_wide.head()

## Fruit   Apple  Banana  Watermelon
## Repeat                           
## A1        4.6     8.7         8.1
## A2        3.9     8.8         8.5
## A3        5.2    10.3         7.5
## A4        6.9    11.5         8.4
## A5        4.8    12.7        10.3

fvalue, pvalue = stats.f_oneway(df_wide['Apple'], df_wide['Banana'], df_wide['Watermelon'])
print(fvalue, pvalue)

## 28.658869785419157 7.5222561940802785e-06

The results indicated that the p value is less than 0.05, which means that the difference between the means of the groups is statistically significant.

# get ANOVA table as R like output
import statsmodels.api as sm
from statsmodels.formula.api import ols

# Ordinary Least Squares (OLS) model
model = ols('Vitamin ~ C(Fruit)', data=df).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table

# ANOVA table using bioinfokit v1.0.3 or later (it uses wrapper script for anova_lm)

##              sum_sq    df         F    PR(>F)
## C(Fruit)  95.567778   2.0  28.65887  0.000008
## Residual  25.010000  15.0       NaN       NaN

from bioinfokit.analys import stat
res = stat()
res.anova_stat(df=df, res_var='Vitamin', anova_model='Vitamin ~ C(Fruit)')
res.anova_summary

##             df     sum_sq    mean_sq         F    PR(>F)
## C(Fruit)   2.0  95.567778  47.783889  28.65887  0.000008
## Residual  15.0  25.010000   1.667333       NaN       NaN

Shapiro-Wilk test can be used to check the normal distribution of residuals

import scipy.stats as stats
w, pvalue = stats.shapiro(model.resid)
print(w, pvalue)

## 0.9351375699043274 0.2388565093278885

As the p value is non significant, we fail to reject null hypothesis and conclude that data is drawn from normal distribution.

perform multiple pairwise comparison (Tukey’s HSD)

# unequal sample size data, tukey_hsd uses Tukey-Kramer test
import warnings
warnings.filterwarnings('ignore')

res = stat()
res.tukey_hsd(df=df, res_var='Vitamin', xfac_var='Fruit', anova_model='Vitamin~ C(Fruit)')
res.tukey_summary

##    group1      group2      Diff     Lower     Upper    q-value   p-value
## 0   Apple      Banana  5.483333  3.547664  7.419003  10.401813  0.001000
## 1   Apple  Watermelon  3.900000  1.964331  5.835669   7.398250  0.001000
## 2  Banana  Watermelon  1.583333 -0.352336  3.519003   3.003563  0.118396